「力扣」第 343 题:“整数拆分”题解
题解地址:“贪心选择”性质的简单证明、记忆化搜索、动态规划 (Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:343. 整数拆分。
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
“贪心选择”性质的简单证明、记忆化搜索、动态规划 (Python 代码、Java 代码)
能够使用“贪心算法”完成的问题,严格上来说,是要证明这个问题具有“贪心选择”性质,但是如果一个问题,不能使用贪心算法,只需要举一个反例就可以了。
而证明一个问题具有“贪心选择”性质,通常是比较困难的。本篇就我对「力扣」第 343 题:“整数拆分”的贪心选择性质给予证明。
方法一:贪心算法
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)
 ),
), ),
),
分析题意
题目中说,把正整数 $n$ 分解成若干个正整数加法因子,让我们求所有可能的加法因子相乘以后乘积的最大值。看示例 2 ,就很清楚题目的意思,这里就不多展开了。
本文对求解这个问题的贪心选择性质做了简单的归纳、证明。即我们要证明的是:
“贪心地”、“尽可能多”地分解出 $3$ 正整这个加法因子,就能够使得最终的乘积得到最大。
从小规模数据找规律
我们不妨从最小的正整数加法因子 $1$ 开始,到 $2$、$3$、$4$、…,依次分析,分解以后,乘积的大小,写几个出来,看看规律。
- 情况 1:如果分解式中含有 $1$
因为 $1 \times (n-1) = n-1 < n$,明显,越分解乘积越小。
结论1:$1$ 不能作为分解的正整数加法因子。
- 情况 2:如果分解式中含有 $2$
直觉上,分解以后相乘肯定比原来这个数要大。例如:$n = 19$ 时,$2 \times 17 = 34 > 19$,越大的数越是如此,因此我们要关心的是边界。于是解不等式
$$2 \times (n - 2) > n$$
得 $n > 4$。
结论2:当 $n > 4$ 的时候,分解出 $2$ 这个因子,与剩下的数 $(n - 2)$ 得到的乘积,就肯定超过 $n$ 了。
- 情况 3:如果分解式中含有 $3$
直觉上,也是分解以后相乘肯定比原来这个数要大。例如:$n = 19$ 时,$3 \times 16 = 48 > 19$,越大的数越是如此,因此我们要关心的是边界。于是解不等式
$$3 \times (n - 3) > n$$
得 $n > 4.5$。
结论3:当 $n > 4.5$ 的时候,分解出 $3$ 这个因子,与剩下的数 $(n - 3)$ 得到的乘积,就肯定超过 $n$ 了。
- 情况 4:如果分解式中含有 $4$
情况就有点意思了,我们就可以比较以下四者的乘积大小:
(1)$n$;
(2)$4 \times (n - 4)$;
(3)$2 \times 2 \times (n - 4)$;
(4)$1 \times 3 \times (n - 4)$,其实这都不用考虑,因为情况 1 的结论:$1$ 不能作为分解的正整数加法因子,因为它会使得乘积原来越小,下面我们马上还会分析到。
在 $n$ 比较大的时候,$4 \times (n - 4) > n$ 是显然的,而 $4 \times (n - 4) = 2 \times 2 \times (n - 4)$,又由上面的第 1 点可知分解出 1 肯定使得乘积越来越小,而且很明显 $4 \times (n - 4) > 1 \times 3 \times (n - 4)$。
结论:
结论4:分解出 $4$,等价于分解出两个 $2$,因此,情况 2 就包含了情况 4 ,故没有必要考虑分解出正整数加法因子 $4$。
- 情况 5:如果分解式中含有 $5$
情况也有点意思了,我们就可以比较以下四者的乘积大小:
(1)$n$;
(2)$5 \times (n - 5)$;
(3)$2 \times 3 \times (n - 5)$;
(4)$1 \times 4 \times (n - 5)$;
在 $n$ 比较大的时候,$5 \times (n - 5) > n$ 是显然的,而 $2 \times 3 \times (n - 5) > 5 \times (n - 4)$,又由上面的第 1 点可知分解出 1 肯定使得乘积越来越小,而且很明显 $2 \times 3 \times (n - 5) > 5 \times (n - 4) > 1 \times 4 \times (n - 5)$。
结论5:分解出 $5$ 与 $(n - 5)$ 的乘积还不如分解出 $2$ 、 $3$ 与 $(n-5)$ 的乘积,因此没有必要考虑分解出正整数加法因子 $5$。
为了避免行文啰嗦,我就直接写最关键的部分了:
- 情况 6:如果分解式中含有 $6$
$$6 \times (n-6)< 2 \times 2 \times 2 \times (n - 6) < 3 \times 3 \times (n - 6)$$
结论:
分解出 $6$ 与 $(n - 6)$ 的乘积还不如分解出 $3$ 、 $3$ 与 $(n-6)$ 的乘积,因此没有必要考虑分解出正整数加法因子 $6$。
写到这里,估计你也看出来了,继续分析下去的结论就是,
$$7 \times (n - 7) < 2 \times 2 \times 3 \times (n - 7) $$
$$8 \times (n - 8) < 2 \times 3 \times 3 \times (n - 8) $$
$$9 \times (n - 8) < 3 \times 3 \times 3 \times (n - 9) $$
结论:
结论6:$4$ 以上(包括 $4$)的正整数加法因子都不必考虑了,因为分解成它们的乘积,都小于分解出合适数量的 $2$ 和 $3$ 相乘以后的乘积。
根据以上分析,正整数加法因子只有 $2$ 和 $3$,在根据我们的直觉,感觉分解出 $3$ 这个正整数加法因子的乘积肯定比分解出 $2$ 这个正整数加法因子的乘积,还以 $n = 19$ 为例,$3 \times 16 = 48 > 34 = 2 \times 17$,按照惯例,找边界,即解不等式
$$ 3 \times (n - 3) \ge 2 \times (n -2) $$
解得 $n \ge 5$。
结论7:分解出 $3$ 比分解出 $2$ 好。
综上所述:
我们应该尽可能分解出 $3$ ,直到最后剩下 $4$ 或者 $2$。
下面我们分析最后剩下几就不能再分出 $3$ 了:
如果最后剩下 $7$ 的话,可以分解成两个 $3$、$3$、$2$;
如果最后剩下 $6$ 的话,可以分解成两个 $3$;
如果最后剩下 $5$ 的话,可以分解成 $3$ 和 $2$;
如果最后剩下 $4$ 的话,不能分解出 $3$ 了,因为最后剩下的正整数加法因子是 $1$,由结论 1 ,这是不允许的;
如果最后剩下 $3$ 的话,不能分解出 $2$ 了,因为剩下是 $1$,由结论 1 ,这是不允许的。
综上所述:
在大于 $4$ 的前提下,尽可能分解出 $3$ 。当 $n \le 4$ 的时候,专门计算一下给出结论就可以了。
以上分析其实并不难,关键要动手写一下,相信聪明的你一定会比我做得更好。
参考代码 1:
Java 代码:
public class Solution {
public int integerBreak(int n) {
if (n <= 2) {
return 1;
}
if (n == 3) {
return 2;
}
if (n == 4) {
return 4;
}
// 接下来就是 n >= 5 的时候的逻辑了
int res = 1;
while (n > 4) {
res *= 3;
n -= 3;
}
res *= n;
return res;
}
}Python 代码:
class Solution:
def integerBreak(self, n):
if n == 2:
return 1
if n == 3:
return 2
if n == 4:
return 4
res = 1
while n > 4:
res *= 3
n -= 3
res *= n
return res方法二:“记忆化搜索”与“动态规划”
思路:先研究递归结构,发现有大量重叠子问题,再实现“记忆化搜索”,最后实现使用“动态规划”。即先“自顶向下”思考,再“自底向上”实现。
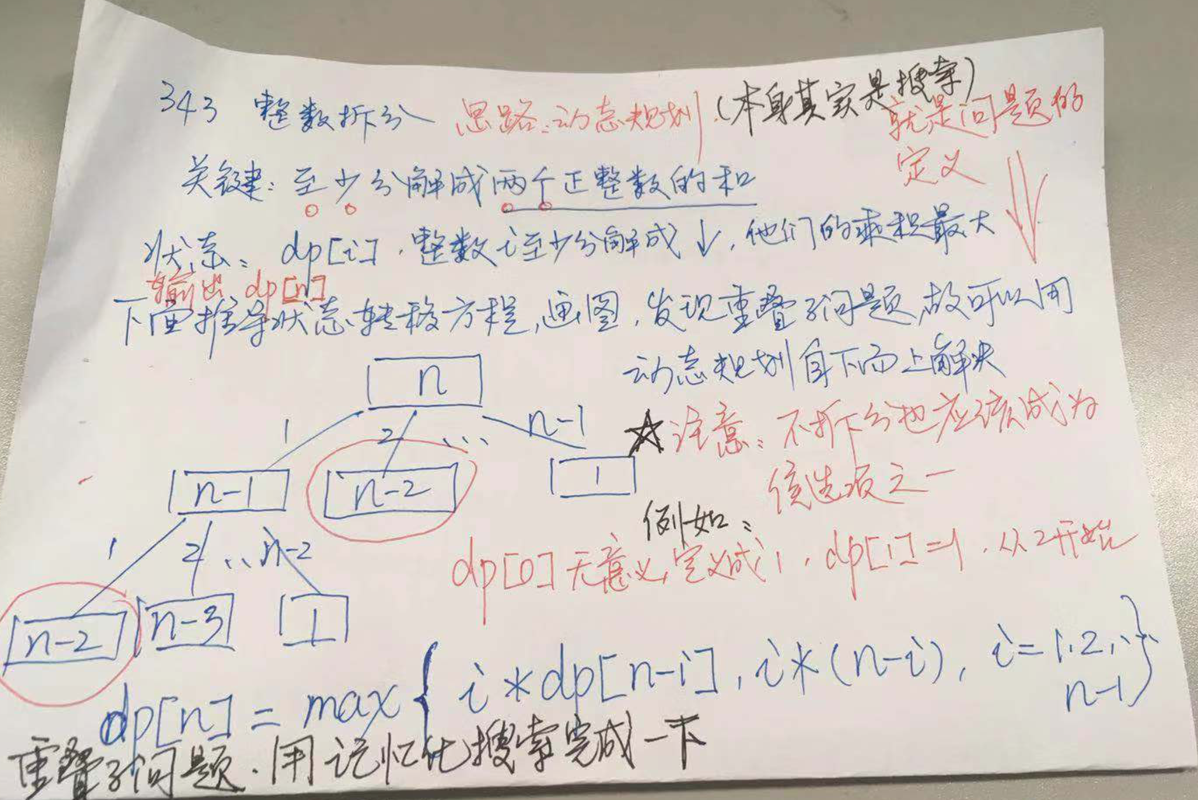
注意:对于每一个状态而言,还要再比较“不再继续分割”和“继续分割”,取当中的最大值,将 $n$ 进行分解的时候,以 $8$ 为例:$1$ 与 $7$ 是一个解,$1$ 与 $7$ 的分解的结果也是一个解。
参考代码 2:记忆化搜索
Python 代码:
class Solution:
def __init__(self):
self.memo = []
def integerBreak(self, n):
self.memo = [-1 for _ in range(n + 1)]
self.memo[0] = 1
self.memo[1] = 1
return self.__dfs(n)
def __dfs(self, n):
if n == 1:
return 1
if self.memo[n] == -1:
res = 0
for i in range(1, n):
res = max(res, i * (n - i), i * self.__dfs(n - i))
self.memo[n] = res
return self.memo[n]Java 代码:
public class Solution {
private int[] memory;
public int integerBreak(int n) {
assert n >= 2;
memory = new int[n + 1];
memory[0] = 0;
memory[1] = 1;
for (int i = 2; i < n + 1; i++) {
memory[i] = -1;
}
int res = breakInteger(n);
return res;
}
// 将 n 进行分割得到的乘积最大值
private int breakInteger(int num) {
if (num == 1) {
return 1;
}
if (memory[num] == -1) {
int res = 0; // 这个初始值可以设置为 0 吗,1 行不行?
for (int i = 1; i < num; i++) {
// 关键之处:状态转移方程,其中 i * (num - i) 这一步很关键,千万不能漏掉
res = max3(res, i * (num - i), i * breakInteger(num - i));
}
memory[num] = res;
}
return memory[num];
}
private int max3(int num1, int num2, int num3) {
int temp = Integer.max(num1, num2);
return Integer.max(temp, num3);
}
public static void main(String[] args) {
Solution2 solution = new Solution2();
int max = solution.integerBreak(9);
System.out.println(max);
}
}参考代码 3:动态规划
Java 代码:
/**
* 动态规划的解法
* Created by liwei on 17/10/3.
*/
public class Solution3 {
private int[] memory;
public int integerBreak(int n) {
memory = new int[n + 1];
memory[0] = 0;
memory[1] = 1;
for (int i = 2; i <= n; i++) {
int maxValue = -1;
for (int j = 1; j <= i - 1; j++) {
maxValue = max3(maxValue, j * (i - j), j * memory[i - j]);
}
memory[i] = maxValue;
}
return memory[n];
}
private int max3(int num1, int num2, int num3) {
int temp = Integer.max(num1, num2);
return Integer.max(temp, num3);
}
public static void main(String[] args) {
Solution3 solution = new Solution3();
int max = solution.integerBreak(9);
System.out.println(max);
}
}Python 代码:
class Solution:
def integerBreak(self, n):
dp = [1 for _ in range(n + 1)]
for i in range(2, n + 1):
for j in range(1, i):
dp[i] = max(dp[i], j * dp[i - j], j * (i - j))
return dp[n]


