「力扣」第 416 题：分割等和子集

发布日期: 2018-05-07

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意:

每个数组中的元素不会超过 100
数组的大小不会超过 200
示例 1:

输入: [1, 5, 11, 5]

输出: true

解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2:

输入: [1, 2, 3, 5]

输出: false

解释: 数组不能分割成两个元素和相等的子集.

关于 0-1 背包问题的介绍，大家可以在互联网上搜索《背包九讲》进行相关知识的学习。本题解有些地方使用了 0-1 背包问题的描述，因此会不加解释的使用“背包”、“容量”这样的名词。

本题解按照动态规划的一般思考方向进行讲解（仅供参考，本人水平有限，大概觉得是这几个方面），它们是：

1、状态定义；

2、状态转移方程；

3、初始化；

4、输出；

5、思考状态压缩。

这 5 个部分是本题解的结构。其它类似的动态规划问题也可以按照这样的方向去思考、解释和理解。

事实上，这是一个典型的“动态规划”问题，并且它的“原形”是“0-1 背包问题”。使用“动态规划”解决问题的思路是“以空间换时间”，“规划”这个词在英文中就是“填表格”的意思，代码执行的过程，也可以称之为“填表格”。

“动态规划”的方法可以认为是为我们提供了一个思考问题的方向，我们不是直接面对问题求解，而是去找原始问题（或者说和原始问题相关的问题）的最开始的样子，通过“状态转移方程”（这里没法再解释了，可以结合下文理解）记录下每一步求解的结果，直到最终问题解决。

而直接面对问题求解，就是我们熟悉的“递归”方法，由于有大量重复子问题，我们就需要加缓存，这叫“记忆化递归”，这里就不给参考代码了，感兴趣的朋友可以自己写一下，比较一下它们两种思考方式的不同之处和优缺点。

做这道题需要做这样一个等价转换：是否可以从这个数组中挑选出一些正整数，使得这些数的和等于整个数组元素的和的一半。前提条件是：数组的和一定得是偶数，即数组的和一定得被 $2$ 整除，这一点是特判。

本题与 0-1 背包问题有一个很大的不同，即：

0-1 背包问题选取的物品的容积总量不能超过规定的总量；
本题选取的数字之和需要恰恰好等于规定的和的一半。

这一点区别，决定了在初始化的时候，所有的值应该初始化为 false。（《背包九讲》的作者在介绍 0-1 背包问题的时候，有强调过这点区别，我在这里也只是再重复一下。）

作为“0-1 背包问题”，它的特点是：“每个数只能用一次”。思路是：物品一个一个选，容量也一点一点放大考虑（这一点是“动态规划”的思想，特别重要）。

如果在实际生活中，其实我们也是这样做的，一个一个尝试把候选物品放入“背包”，看什么时候能容纳的价值最大。

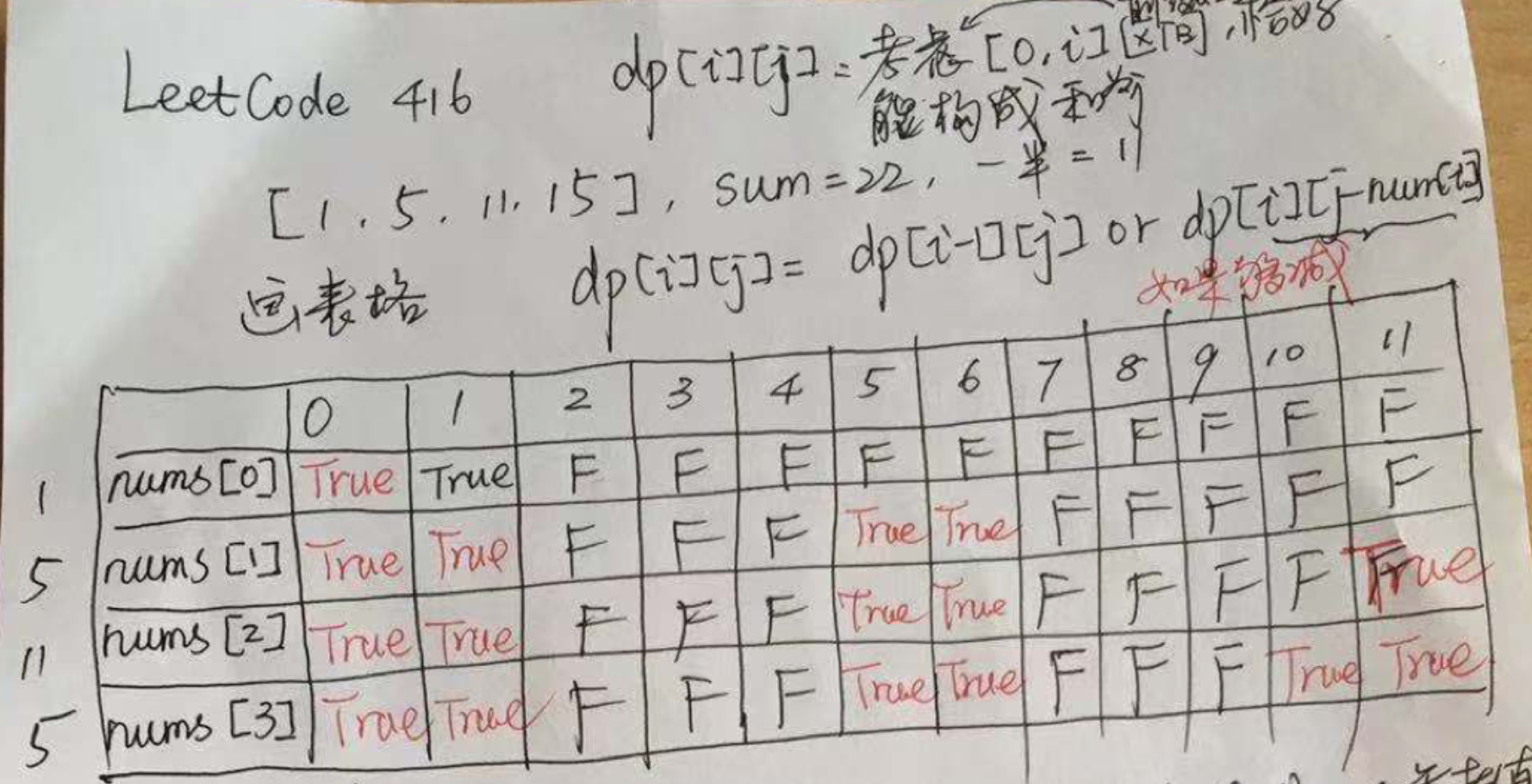
具体做法是：画一个 len 行，target + 1 列的表格。这里 len 是物品的个数，target 是背包的容量。len 行表示一个一个物品考虑，target + 1多出来的那 1 列，表示背包容量从 0 开始，很多时候，我们需要考虑这个容量为 0 的数值。

状态定义：dp[i][j]表示从数组的 [0, i] 这个子区间内挑选一些正整数，每个数只能用一次，使得这些数的和恰好等于 j。
状态转移方程：很多时候，状态转移方程思考的角度是“分类讨论”，对于“0-1 背包问题”而言就是“当前考虑到的数字选与不选”。

1、不选择 nums[i]，如果在 [0, i - 1] 这个子区间内已经有一部分元素，使得它们的和为 j ，那么 dp[i][j] = true；

2、选择 nums[i]，如果在 [0, i - 1] 这个子区间内就得找到一部分元素，使得它们的和为 j - nums[i]。

状态转移方程是：

dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i]]

一般写出状态转移方程以后，就需要考虑边界条件（一般而言也是初始化条件）。

1、j - nums[i] 作为数组的下标，一定得保证大于等于 0 ，因此 nums[i] <= j；
2、注意到一种非常特殊的情况：j 恰好等于 nums[i]，即单独 nums[j] 这个数恰好等于此时“背包的容积” j，这也是符合题意的。

因此完整的状态转移方程是：

$$
\text{dp}[i][j]=
\begin{cases}
\text{dp}[i - 1][j], & 至少是这个答案，如果 \ \text{dp}[i - 1][j] \ 为真，直接计算下一个状态 \
\text{true}, & \text{nums[i] = j} \
\text{dp}[i - 1][j - nums[i]]. & \text{nums[i] < j}
\end{cases}
$$

说明：虽然写成花括号，但是它们的关系是或者。

初始化：dp[0][0] = false，因为是正整数，当然凑不出和为 0。
输出：dp[len - 1][target]，这里 len 表示数组的长度，target 是数组的元素之和（必须是偶数）的一半。

参考代码 1：

public class Solution {

    public boolean canPartition(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return false;
        }

        int sum = 0;
        for (int num : nums) {
            sum += num;
        }

        // 特判：如果是奇数，就不符合要求
        if ((sum & 1) == 1) {
            return false;
        }

        int target = sum / 2;

        // 创建二维状态数组，行：物品索引，列：容量（包括 0）
        boolean[][] dp = new boolean[len][target + 1];

        // 先填表格第 0 行，第 1 个数只能让容积为它自己的背包恰好装满
        if (nums[0] <= target) {
            dp[0][nums[0]] = true;
        }

        // 再填表格后面几行
        for (int i = 1; i < len; i++) {
            for (int j = 0; j <= target; j++) {
                // 直接从上一行先把结果抄下来，然后再修正
                dp[i][j] = dp[i - 1][j];

                if (nums[i] == j) {
                    dp[i][j] = true;
                    continue;
                }
                if (nums[i] < j) {
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
                }
            }
        }
        return dp[len - 1][target];
    }
}

复杂度分析：

时间复杂度：$O(NC)$：这里 $N$ 是数组元素的个数，$C$ 是数组元素的和的一半。
空间复杂度：$O(NC)$。

下面是几点说明：

1、修改状态数组初始化的定义：dp[0][0] = true。

注意到：容量为 0 的时候，即 dp[i][0] 按照本意来说，应该设置为 false ，但是注意到状态转移方程（代码中）：

dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];

j - nums[i] == 0 成立的时候，根据上面分析，就说明单独的 nums[i] 这个数就恰好能够在被分割为单独的一组，其余的数分割成为另外一组，因此，我们把初始化的 dp[i][0] 设置成为 true 在代码运行层面是完全没有问题的。

2、观察状态转移方程的特点，or 的结果只要为真，表格下面所有的值都为真，因此在填表的时候，只要表格的最后一列是 true，代码就可以结束，直接返回 true 即可。

参考代码 2：

public class Solution {

    public boolean canPartition(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return false;
        }

        int sum = 0;
        for (int num : nums) {
            sum += num;
        }

        if ((sum & 1) == 1) {
            return false;
        }

        int target = sum / 2;

        boolean[][] dp = new boolean[len][target + 1];
        // 初始化成为 true 虽然不符合状态定义，但是从状态转移来说是完全可以的
        dp[0][0] = true;

        if (nums[0] <= target) {
            dp[0][nums[0]] = true;
        }

        for (int i = 1; i < len; i++) {
            for (int j = 0; j <= target; j++) {

                dp[i][j] = dp[i - 1][j];

                if (nums[i] <= j) {
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
                }
            }

            // 由于状态转移方程的特殊性，提前结束，可以认为是剪枝操作
            if (dp[i][target]) {
                return true;
            }
        }
        return dp[len - 1][target];
    }
}

复杂度分析：(同上)

3、“0-1 背包问题”常规优化：“状态数组”从二维降到一维，减少空间复杂度。

在“填表格”的时候，当前行只参考了上一行的值，因此状态数组可以只设置 $2$ 行，使用“滚动数组”的技巧“填表格”即可；
实际上连“滚动数组”都不必，在“填表格”的时候，当前行总是参考了它上面一行 “头顶上” 那个位置和“左上角”某个位置的值。因此，我们可以只开一个一维数组，从后向前依次填表即可。

这一点第 1 次接触的时候，可能会觉得很奇怪，理解的办法是，就拿题目中的示例，画一个表格，自己模拟一遍程序是如何“填表”的行为，就很清楚为什么状态数组压缩到 1 行的时候，需要“从后前向”填表。

“从后向前” 写的过程中，一旦 nums[i] <= j 不满足，可以马上退出当前循环，因为后面的 j 的值肯定越来越小，没有必要继续做判断，直接进入外层循环的下一层。相当于也是一个剪枝，这一点是“从前向后”填表所不具备的。

参考代码 3：只展示了状态数组压缩到一维，并且“从后向前”填表格的代码。

public class Solution {

    public boolean canPartition(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return false;
        }

        int sum = 0;
        for (int num : nums) {
            sum += num;
        }

        if ((sum & 1) == 1) {
            return false;
        }

        int target = sum / 2;

        boolean[] dp = new boolean[target + 1];
        dp[0] = true;

        if (nums[0] <= target) {
            dp[nums[0]] = true;
        }

        for (int i = 1; i < len; i++) {
            for (int j = target; nums[i] <= j; j--) {
                if (dp[target]) {
                    return true;
                }

                dp[j] = dp[j] || dp[j - nums[i]];
            }
        }
        return dp[target];
    }
}