「力扣」第 72 题：编辑距离（困难）

发布日期: 2018-04-13

链接：https://leetcode-cn.com/problems/edit-distance
题解链接：https://leetcode-cn.com/problems/edit-distance/solution/dong-tai-gui-hua-java-by-liweiwei1419/

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数。

你可以对一个单词进行如下三种操作：

插入一个字符

删除一个字符

替换一个字符

示例 1：
输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2：
输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

这个问题是使用「动态规划」解决的的经典问题，一般是作为例题进行学习的，因此就直接给出「动态规划」方法的解释，主要在理解「动态规划」是如何定义「状态」和推导「状态转移方程」。

思路：

「动态规划」告诉我们可以「自底向上」去考虑一个问题，思路是：先想这个问题最开始是什么情况，这个问题是两个字符串都为空字符的时候，然后逐个地，一个字符一个字符加上去，在加字符的过程中考虑「状态转移」；
由于要考虑空字符，因此状态空间要多设置一行、多设置一列。

方法：动态规划

第 1 步：定义状态

状态：dp[i][j] 表示将 word1[0, i) 转换成为 word2[0, j) 的方案数。

思考状态的方法：1、题目问什么就将什么定义为状态；2、「状态转移方程」怎么好推导，就怎么定义状态；3、根据经验和问题的特点（只有多做题了）。

说明：由于要考虑空字符，这里的下标 i 不包括 word[i]，同理下标 j 不包括 word[j]，从行数和列数多设置一行、一列也可以来理解这一点，也就是状态的下标 i 和 j 和字符的下标 i、j 有一个位置的偏差。

下文有些地方是 ) 有些地方是 ] 。如果造成疑惑，可以暂时不管，并不影响理解思想。

第 2 步：思考状态转移方程

状态转移方程通常是在做分类讨论，而分类讨论的过程，常常利用了这个问题的「最优子结构」。

情况 1：`word1[i] == word2[j]`

如果 word1[i] == word2[j] 成立，则将 word1[0, i) 转换成为 word2[0, j) 的方案数就等于将 word1[0, i - 1) 转换成为 word2[0, j - 1) 的方案数，即：

dp[i + 1][j + 1] = dp[i][j]；

注意：这种情况，方案数最少，后面三种情况可以不用再讨论。

直觉：后面的情况要考虑的字符更多，并且还会增加 1 步操作；
实验：从实际代码运行的结果上看，可以通过测评，并且的确是后面的情况不会使得结果更少，大家还可以使用 aaaa 和 aaaaa 这样的情况去验证。

对于这个结论 @1dUv8IogjC 这位朋友给出了使用「数学归纳法」的证明，欢迎大家在评论区围观，感谢这位朋友。

也可以参考 @gelthin 这位朋友给出的题解：《证明: 当 w1[i] == w2[j]时，必有 DP[i+1][j+1] = DP[i][j]》。

情况 2：`word1[i] != word2[j]`

（下面的文字看过去文绉绉的，意会就可以了，建议尝试自己举例去理解。）

如果 word1[i] != word2[j] ，则将 word1[0, i) 转换成为 word2[0, j) 的方案数就等于下面 3 种情况的最少操作数（「最优子结构」）：

考虑修改 word1[i] 成为 word2[j]；

此时 dp[i + 1][j + 1] = dp[i][j] + 1，这里的 1 代表了将 word1[i] 替换成为 word2[j] 这一步操作。

考虑将 word1[0, i] 的最后一个字符删除；

此时 word1[0, i - 1] 到 word2[0, j] 的最少操作数 $+ 1$，就是这种方案数的最少操作数，即： dp[i + 1][j + 1] = dp[i][j + 1] + 1，这里的 1 代表了 word1[0, i] 的最后一个字符删除这一步操作。

考虑将 word1[0, i] 的末尾添加一个字符使得 word1[i + 1] == word2[j]；

此时考虑方案的时候，由于 word1[i + 1] == word2[j]，状态转移就不应该考虑 word2[j]，因此 word1[0, i] 到 word2[0, j - 1] 的最少操作数 $+ 1$，就是这种方案数的最少操作数，即： dp[i + 1][j + 1] = dp[i + 1][j] + 1，这里的 1 代表了将 word1[0, i] 的末尾添加一个字符使得 word1[i + 1] == word2[j]。（注意：可以考虑一下为什么得先讨论 word1[i] == word2[j] 的情况。）

在这 3 种操作中取最小值。

dp[i + 1][j + 1] = min(dp[i][j], dp[i][j + 1], dp[i + 1][j]) + 1

第 3 步：初始化

从一个字符串变成空字符串，非空字符串的长度就是编辑距离；
以下代码其实就是在填表格的第 $0$ 行、第 $0$ 列。

for (int i = 0; i <= len1; i++) {
    dp[i][0] = i;
}

for (int j = 0; j <= len2; j++) {
    dp[0][j] = j;
}

第 4 步：思考输出

输出：dp[len1][len2] 符合语义，即 word1[0, len) 转换成 word2[0, len2) 的最小操作数。（这里 ) 表示开区间。）

第 5 步：思考状态压缩

我们看一下「状态转移方程」：

如果末尾字符相等，就「抄」左上角单元格的值；
如果末尾字符不相等，就从「正上方」、「左边」、「左上角」三个单元格的值中选出最小的 + 1。

因此，初看可以使用「滚动数组」，更极端一点，用 $2 \times 2$ 表格就可以完成操作。但是真正去做「状态压缩」的时候，由于初始化的原因，发现没有那么容易，在这里不做「状态压缩」。（事实上可以压缩，但是只要是压缩状态，必然给编码造成一定困难，并且破坏代码可读性，根据情况做吧，个人觉得在空间紧张的情况下必须压缩空间，其余不必。）

建议：自己动手填表格，加深体会「动态规划」的「自底向上」填表格解决问题的方法，它不是直接针对问题求解，而是从一个最小的情况开始，逐步递推，并且记录中间过程，得到最终答案的过程。

说明：手动填一下这张表格，体会：

在末尾的两个字符相等的情况下，直接把左上角的值抄下来；

{:width=”220px”}

在末尾的两个字符不相等的情况下，「正上方」、「左边」、「左上角」三个单元格的值中选出最小的 + 1

{:width=”200px”}

手填的时候一不小心很容易出错，然后去比对正确的表格，看看是哪里出错了。

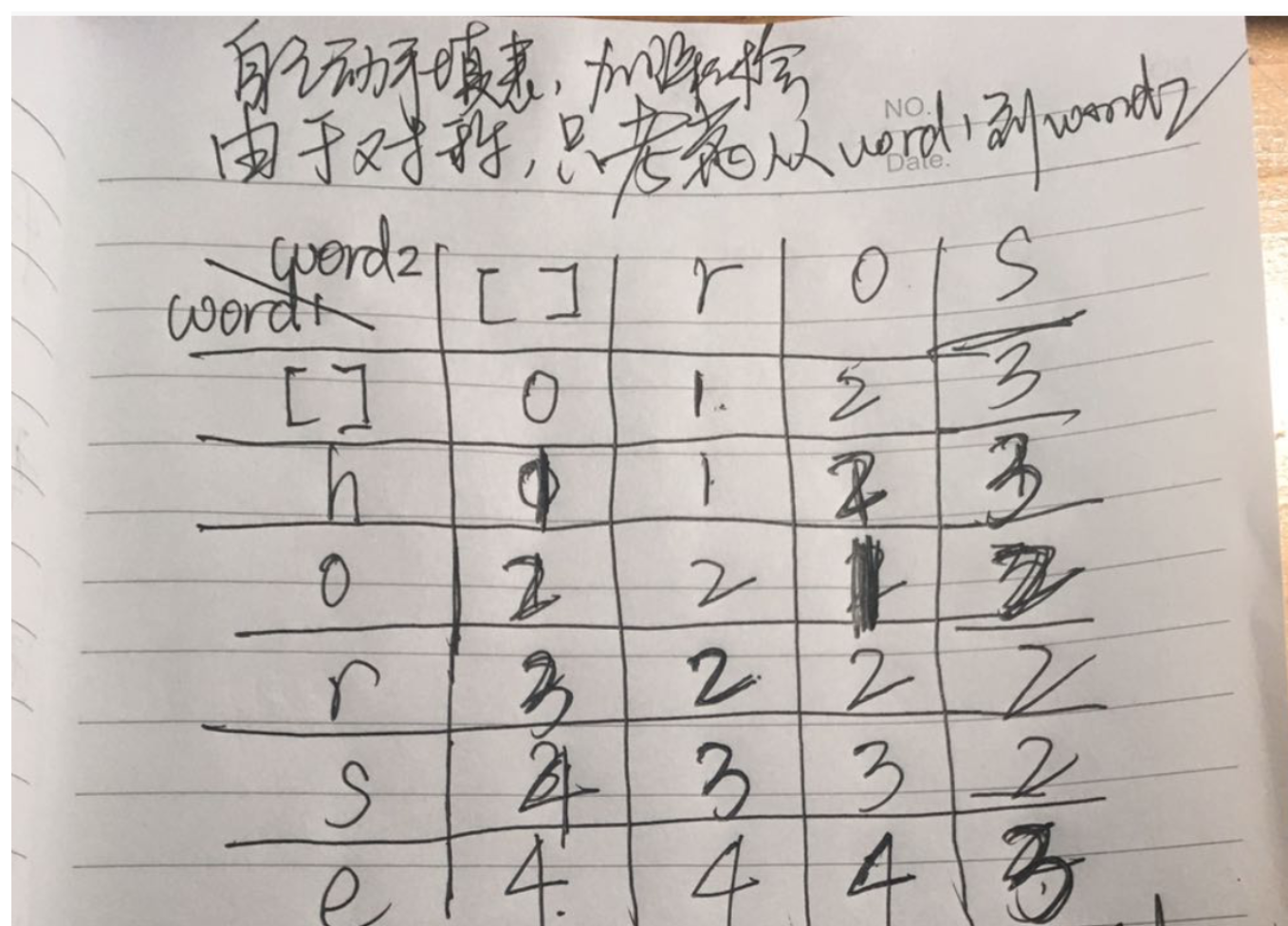
输出：

[0, 1, 2, 3]
[1, 1, 2, 3]
[2, 2, 1, 2]
[3, 2, 2, 2]
[4, 3, 3, 2]
[5, 4, 4, 3]

发现有一个地方填错了，然后去思考原因。

类似问题

这其实是一类称之为区间型 dp 的问题，主要特征是：思考的时候可以先将大区间拆分成小区间，求解的时候由小区间的解得到大区间的解。大家可以做一下这些问题以加深体会做这一类问题的思路和技巧，体会可以使用「动态规划」求解的问题的三个特征：

重叠子问题；
最优子结构；
无后效性。

「力扣」上比较典型的区间型 dp 问题有：

「力扣」第 5 题：最长回文子串；
「力扣」第 1143 题：最长公共子串；
「力扣」第 877 题：石子游戏；
「力扣」第 10 题：正则表达式匹配。

参考代码：

import java.util.Arrays;

public class Solution {

    public int minDistance(String word1, String word2) {
        // 由于 word1.charAt(i) 操作会去检查下标是否越界，因此
        // 在 Java 里，将字符串转换成字符数组是常见额操作

        char[] word1Array = word1.toCharArray();
        char[] word2Array = word2.toCharArray();

        int len1 = word1Array.length;
        int len2 = word2Array.length;

        // 多开一行一列是为了保存边界条件，即字符长度为 0 的情况，这一点在字符串的动态规划问题中比较常见
        int[][] dp = new int[len1 + 1][len2 + 1];

        // 初始化：当 word 2 长度为 0 时，将 word1 的全部删除
        for (int i = 1; i <= len1; i++) {
            dp[i][0] = i;
        }
        // 当 word1 长度为 0 时，就插入所有 word2 的字符
        for (int j = 1; j <= len2; j++) {
            dp[0][j] = j;
        }

        // 注意：填写 dp 数组的时候，由于初始化多设置了一行一列，横、纵坐标有个偏移
        for (int i = 0; i < len1; i++) {
            for (int j = 0; j < len2; j++) {
                // 这是最佳情况
                if (word1Array[i] == word2Array[j]) {
                    dp[i + 1][j + 1] = dp[i][j];
                    continue;
                }

                // 否则在以下三种情况中选出步骤最少的，这是「动态规划」的「最优子结构」
                // 1、在下标 i 处插入一个字符
                int insert = dp[i + 1][j] + 1;
                // 2、替换一个字符
                int replace = dp[i][j] + 1;
                // 3、删除一个字符
                int delete = dp[i][j + 1] + 1;
                dp[i + 1][j + 1] = Math.min(Math.min(insert, replace), delete);

            }
        }

        // 打印状态表格进行调试
//        for (int i = 0; i <=len1; i++) {
//            System.out.println(Arrays.toString(dp[i]));
//        }
        return dp[len1][len2];
    }

    public static void main(String[] args) {
        String word1 = "horse";
        String word2 = "ros";

        Solution solution = new Solution();
        int res = solution.minDistance(word1, word2);
        System.out.println(res);
    }
}

复杂度分析：

时间复杂度：$O(MN)$，其中 $M$ 为 word1 的长度，$N$ 为 word2 的长度；
空间复杂度：$O(MN)$，状态表格的大小。

动态规划基础问题整理

「动态规划」问题没有套路，请大家根据情况掌握自己需要的部分，多做一些问题或许是有用的。

第 1 部分：「动态规划」基本问题

递归 + 记忆化：记忆化递归（记忆化搜索），这是「自上而下」的思路；
掌握「自底向上」递推求解问题的方法；
理解「重复子问题」、「最优子结构」、「无后效性」；
掌握「状态定义」、「状态转移方程」

题目序号	题解	知识点	代码
509. 斐波那契数（简单）		递归做一定要加缓存。
70. 爬楼梯（简单）	CSDN	和斐波拉契数是同一道问题。

第 2 部分：最优子结构

题目序号	题解	知识点	代码
279. 完全平方数（中等）
322. 零钱兑换（中等）	动态规划、使用「完全背包」问题思路、图的广度优先遍历
343. 整数拆分（中等）	“贪心选择”性质的简单证明、记忆化搜索、动态规划（Python、Java）

第 3 部分：无后效性

题目序号	题解	知识点	代码
198. 打家劫舍（简单）		二维状态消除后效性
62. 不同路径（中等）
63. 不同路径 II（中等）

第 4 部分：经典问题（1）

题目序号	题解	知识点
53. 最大子序和	动态规划、分治法、CSDN	1、经典动态规划问题；2、分治
300. 最长上升子序列	动态规划、贪心算法 + 二分
5. 最长回文子串	Manacher 算法 + 动态规划（Java、C++、Python）	使用动态规划的方法得到子串的回文性质
72. 编辑距离	动态规划（Java）、CDSN
120. 三角形最小路径和（中等）
10. 正则表达式匹配（困难）
#### 第 5 部分：经典问题（2）背包问题

题目序号	题解	知识点
416. 分割等和子集	动态规划（0-1 背包问题）	很重要的动态规划模型，必须掌握
518. 零钱兑换 II	动态规划（套用完全背包问题模型）
322. 零钱兑换（中等）	动态规划、使用「完全背包」问题思路、图的广度优先遍历
377. 组合总和 Ⅳ	动态规划
494. 目标和		0-1 背包问题
474. 一和零	动态规划（转换为 0-1 背包问题）

第 6 部分：经典问题（3）股票问题

题目序号	题解	知识点
121. 买卖股票的最佳时机（简单）	暴力枚举 + 动态规划 + 差分思想、CSDN
122. 买卖股票的最佳时机 II（简单）	暴力搜索 + 贪心算法 + 动态规划、CSDN
123. 买卖股票的最佳时机 III（困难）	动态规划、CSDN	1、从后向前写可以把状态压缩到一维；2、分解成两个 121 题。
188. 买卖股票的最佳时机 IV（困难）	动态规划
309. 最佳买卖股票时机含冷冻期（中等）	动态规划
714. 买卖股票的最佳时机含手续费（中等）	动态规划

liweiwei419

https://liweiwei1419.gitee.io/leetcode-algo/2018/04/13/leetcode-algo/0072-edit-distance/

本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 liweiwei419 !

滑动窗口哈希表动态规划

「力扣」第 91 题：解码方法（中等）

「力扣」第 91 题：解码方法（中等） 1、画图；2、分类（用加法）、分步（用乘法）链接题解链接要求：一条包含字母 A-Z 的消息通过以下方式进行了编码： 'A' -> 1 'B' -&g

2018-04-14 专题 15：动态规划

字符串动态规划

「力扣」第 70 题：爬楼梯

「力扣」第 70 题：爬楼梯斐波拉契数列，画出树形结构，发现大量重叠子问题。「动态规划」告诉我们「自顶向上」求解问题的思路。链接英文地址假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有

2018-04-12 专题 15：动态规划

动态规划

「力扣」第 72 题：编辑距离（困难）