「二叉树」专题 2:反转一棵二叉树
注:这一节练习 3 和练习 4 都是很经典的问题。
和二叉树相关的问题,在面试中是非常常见的。一旦我们熟悉了这些问题以后,会发现这些问题其实是非常简单的。
「力扣」第 226 题:反转一棵二叉树
中文网址:226. 翻转二叉树 ;
英文网址:226. Invert Binary Tree 。
翻转一棵二叉树。
示例:
输入:
4 / \ 2 7 / \ / \ 1 3 6 9输出:
4 / \ 7 2 / \ / \ 9 6 3 1备注:
这个问题是受到 Max Howell 的 原问题 启发的 :谷歌:我们90%的工程师使用您编写的软件(Homebrew),但是您却无法在面试时在白板上写出翻转二叉树这道题,这太糟糕了。
分析:算法是非常重要的基本功。即使是大公司都非常注重基础问题的考察。
这道问题可以说是一个经典的问题。LeetCode 上有如下备注:
这个问题是受到 Max Howell 的 原问题 启发的 :
谷歌:我们90%的工程师使用您编写的软件(Homebrew),但是您却无法在面试时在白板上写出翻转二叉树这道题,这太糟糕了。
思路1:我们可以使用递归方法来完成,我们写好之后,会发现其实就是完成了一次深度优先遍历,并且是前序遍历,有的朋友可能写出来的后序遍历,那么我们不禁要问,中序遍历可不可以,答案是不可以,因为中序遍历很可能一个结点会被翻转两次,这与我们的要求是违背的。
Java 代码:
Java 代码:后序遍历
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
invertTree(root.left);
invertTree(root.right);
// swap root.left 和 root.right
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
return root;
}
}Java 代码:与上面的代码等价
public class Solution2 {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return root;
}
TreeNode left = root.left;
TreeNode right = root.right;
root.left = invertTree(right);
root.right = invertTree(left);
return root;
}
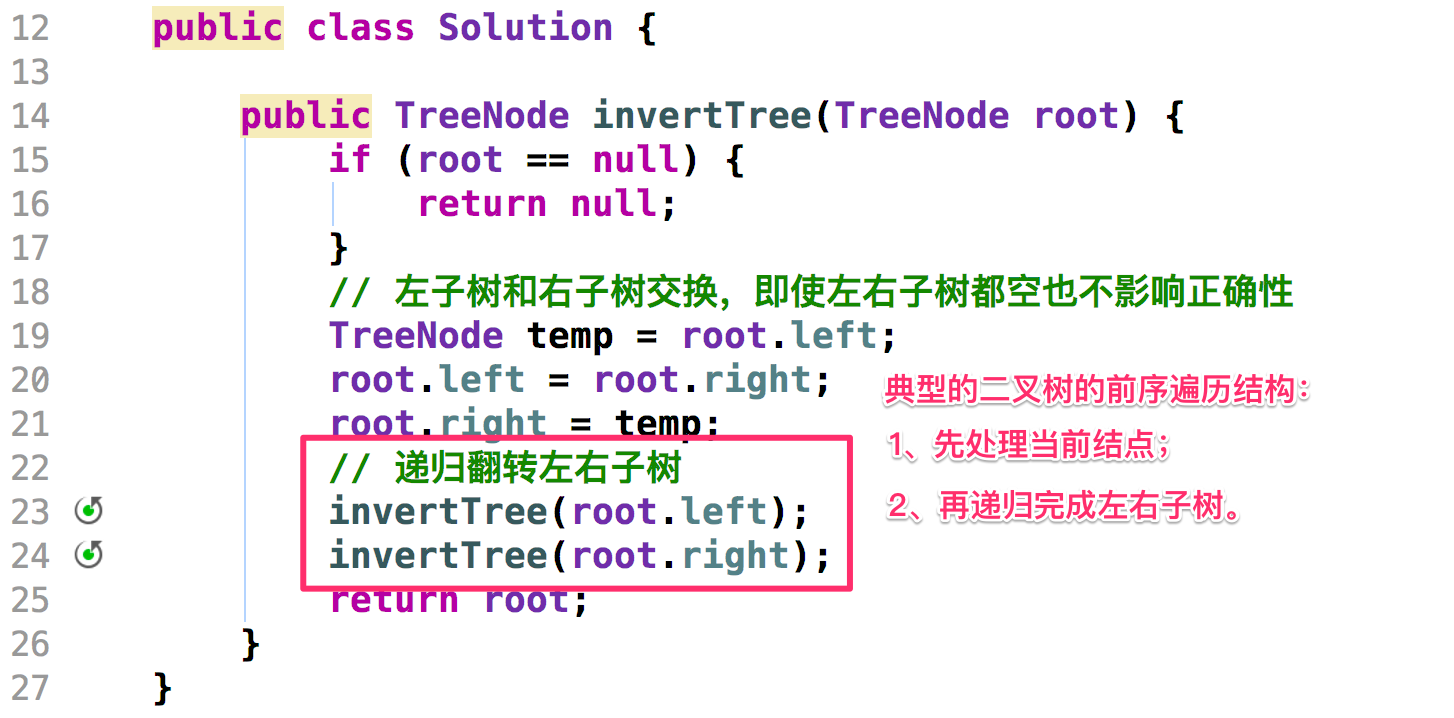
}方法一:前序遍历
Java 代码:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
// 左子树和右子树交换,即使左右子树都空也不影响正确性
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
// 递归翻转左右子树
invertTree(root.left);
invertTree(root.right);
return root;
}
}方法二:中序遍历
注意:写中序遍历的时候,不能仅仅只是将前序遍历的代码顺序调整一下。
因为在“中序遍历”的时候,左右子树已经交换过了,因此原来写 invertTree(root.right); 的地方,应该写作 invertTree(root.left);。
Java 代码:
public class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
invertTree(root.left);
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
// 注意:因为左右子树已经交换了,因此这里不能写 invertTree(root.right);
invertTree(root.left);
return root;
}
}
方法三:后序遍历
Java 代码:
public class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
invertTree(root.left);
invertTree(root.right);
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
return root;
}
}方法四:层序遍历
Java 代码:
import java.util.LinkedList;
import java.util.Queue;
public class Solution {
public TreeNode invertTree(TreeNode root) {
// 结点为空的特殊情况要先考虑
if (root == null) {
return null;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode curNode = queue.poll();
// 只要其中之一非空,我都交换,并且把非空的结点添加到队列里
if (curNode.left != null || curNode.right != null) {
// 先翻转
TreeNode temp = curNode.left;
curNode.left = curNode.right;
curNode.right = temp;
// 把非空的节点加入队列
if (curNode.left != null) {
queue.offer(curNode.left);
}
if (curNode.right != null) {
queue.offer(curNode.right);
}
}
}
return root;
}
}



