「力扣」第 1319 题：等式方程的可满足性（中等）

专题 11：并查集

发布日期: 2017-11-04

「力扣」第 1319 题：连通网络的操作次数（中等）

连通性问题，比较容易想到使用并查集，并查集在写的时候，可以尽量封装起来，以凸显主干逻辑。并且路径压缩与按 rank 合并这两个优化技巧，选择其中一个即可。

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。

网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。

给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。

示例 1：
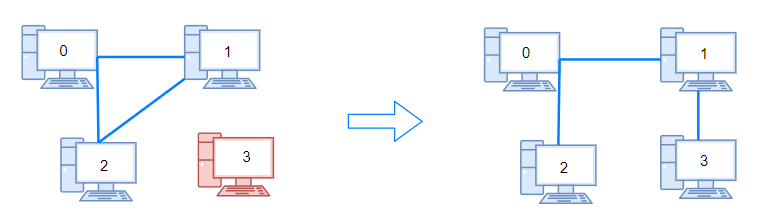
输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。
示例 2：
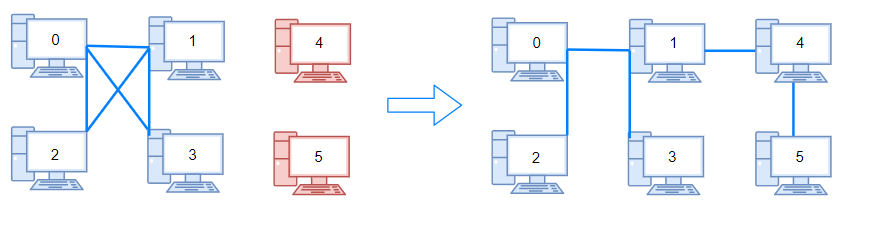
输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
输出：2
示例 3：
输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
输出：-1
解释：线缆数量不足。
示例 4：
输入：n = 5, connections = [[0,1],[0,2],[3,4],[2,3]]
输出：0
提示：

1 <= n <= 10^5

1 <= connections.length <= min(n*(n-1)/2, 10^5)

connections[i].length == 2

0 <= connections[i][0], connections[i][1] < n

connections[i][0] != connections[i][1]

没有重复的连接。

两台计算机不会通过多条线缆连接。

思路：

记录一个变量，表示多余的边；
在合并的时候，返回是否合并成功。如果合并不成功，表示在一个连通分量里，这条边是多余的边（用于以后连接独立的连通分量）；
如果多余的边不够剩余的连通分量个数，返回 -1；如果够用，每用一条边都可以减少一个连通分量的个数；
否则多余的边数够用，返回连通分量 -1 即可（减去的这个 1 是最大的那个连通分量）。

参考代码：

Java 代码：

public class Solution {

    public int makeConnected(int n, int[][] connections) {
        // 特判
        if (connections.length < n - 1) {
            return -1;
        }

        UnionFind unionFind = new UnionFind(n);

        // 多余的边的条数
        int cnt = 0;

        for (int[] connection : connections) {
            boolean success = unionFind.union(connection[0], connection[1]);
            if (!success) {
                cnt++;
            }
        }

        // 特判
        if (unionFind.count == 1) {
            return 0;
        }

        // 扣掉的 1 是当前结点数最大的连通分量
        if (cnt < unionFind.count - 1) {
            return -1;
        }
        return unionFind.count - 1;
    }

    private class UnionFind {
        /**
         * 父亲结点标识数组
         */
        private int[] parent;
        /**
         * 连通分量个数
         */
        private int count;

        public UnionFind(int n) {
            count = n;
            parent = new int[n];
            for (int i = 0; i < n; i++) {
                parent[i] = i;
            }
        }

        public int find(int x) {
            while (x != parent[x]) {
                // 路径压缩（隔代压缩）
                parent[x] = parent[parent[x]];
                x = parent[x];
            }
            return x;
        }

        /**
         * @param x
         * @param y
         * @return 是否合并成功，如果 x 和 y 本来就在一个连通分量里，返回 false
         */
        public boolean union(int x, int y) {
            int rootX = find(x);
            int rootY = find(y);

            if (rootX == rootY) {
                return false;
            }

            parent[rootX] = rootY;
            count--;
            return true;
        }
    }
}