「力扣」第 952 题：按公因数计算最大组件大小（困难）

「力扣」第 952 题：按公因数计算最大组件大小（困难）

• 链接
• 题解链接

给定一个由不同正整数的组成的非空数组 A，考虑下面的图：

• 有 A.length 个节点，按从 A[0] 到 A[A.length - 1] 标记；
• 只有当 A[i] 和 A[j] 共用一个大于 1 的公因数时，A[i] 和 A[j] 之间才有一条边。

返回图中最大连通组件的大小。

示例 1：

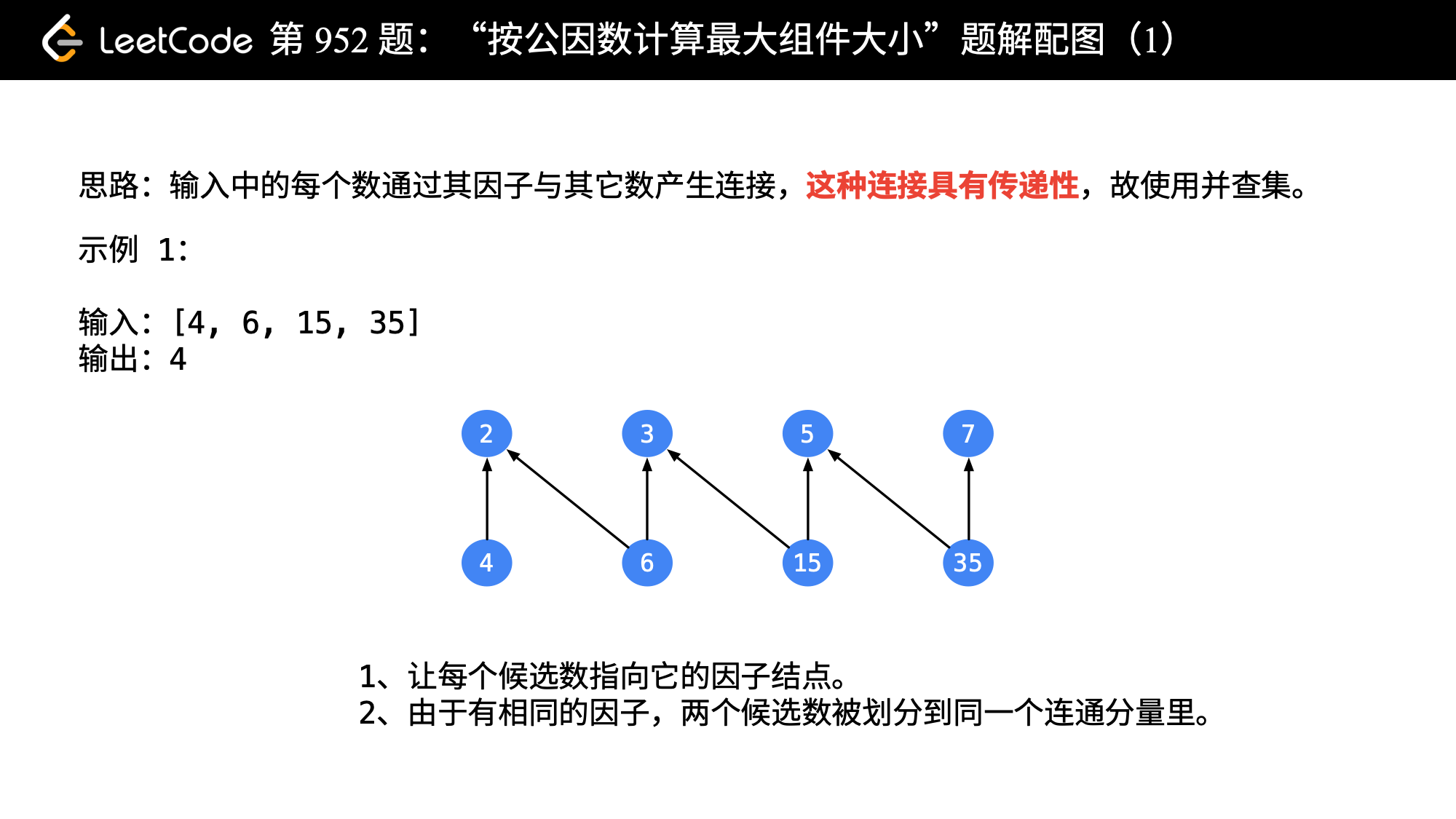
输入：[4,6,15,35]
输出：4

示例 2：

输入：[20,50,9,63]
输出：2

示例 3：

输入：[2,3,6,7,4,12,21,39]
输出：8

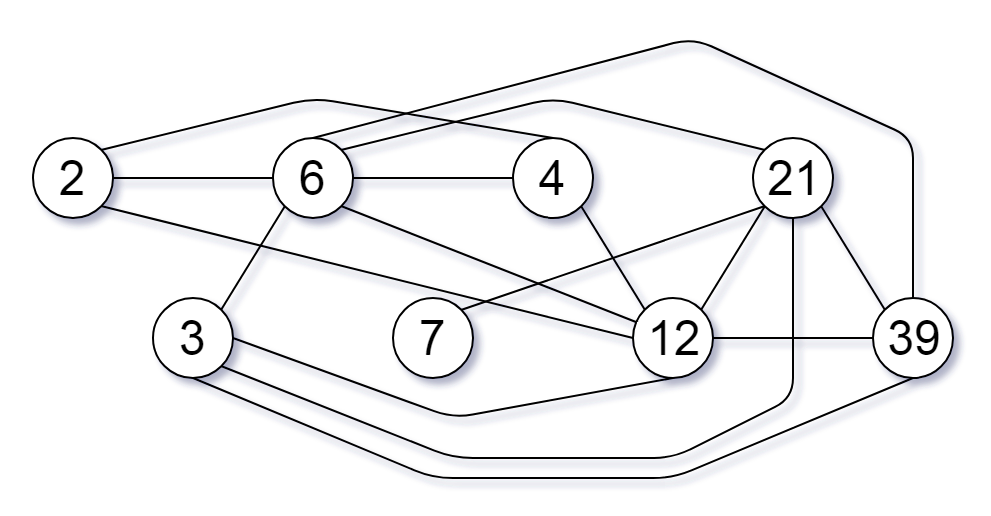
提示：

1. 1 <= A.length <= 20000
2. 1 <= A[i] <= 100000

这道题题目都直接画成了连通图，显然可以考虑使用并查集。

1、这些数的所有质因子，是连接不同候选数的桥梁，即两个数因为有了相同的质因子，它们才能在一个连通分量里；

2、最大连通组件那里，要绕一个弯子，对于候选数组中的每一个数，查询一下这个数在并查集中的代表元（即根结点是谁），然后做一个计数统计，记录那个出现最多的代表元的个数即可。

参考代码：

Java 代码：

public class Solution {

    public int largestComponentSize(int[] A) {
        int maxVal = 0;
        for (int num : A) {
            maxVal = Math.max(maxVal, num);
        }

        // 0 位置不使用，因此需要 + 1
        UnionFind unionFind = new UnionFind(maxVal + 1);

        for (int num : A) {
            double upBound = Math.sqrt(num);
            for (int i = 2; i <= upBound; i++) {
                if (num % i == 0) {
                    unionFind.union(num, i);
                    unionFind.union(num, num / i);
                }
            }
        }

        // 将候选数组映射成代表元，统计代表元出现的次数，找出最大者
        int[] cnt = new int[maxVal + 1];
        int res = 0;
        for (int num : A) {
            int root = unionFind.find(num);
            cnt[root]++;
            res = Math.max(res, cnt[root]);
        }
        return res;
    }

    private class UnionFind {

        private int[] parent;

        public UnionFind(int n) {
            parent = new int[n];
            for (int i = 0; i < n; i++) {
                parent[i] = i;
            }
        }

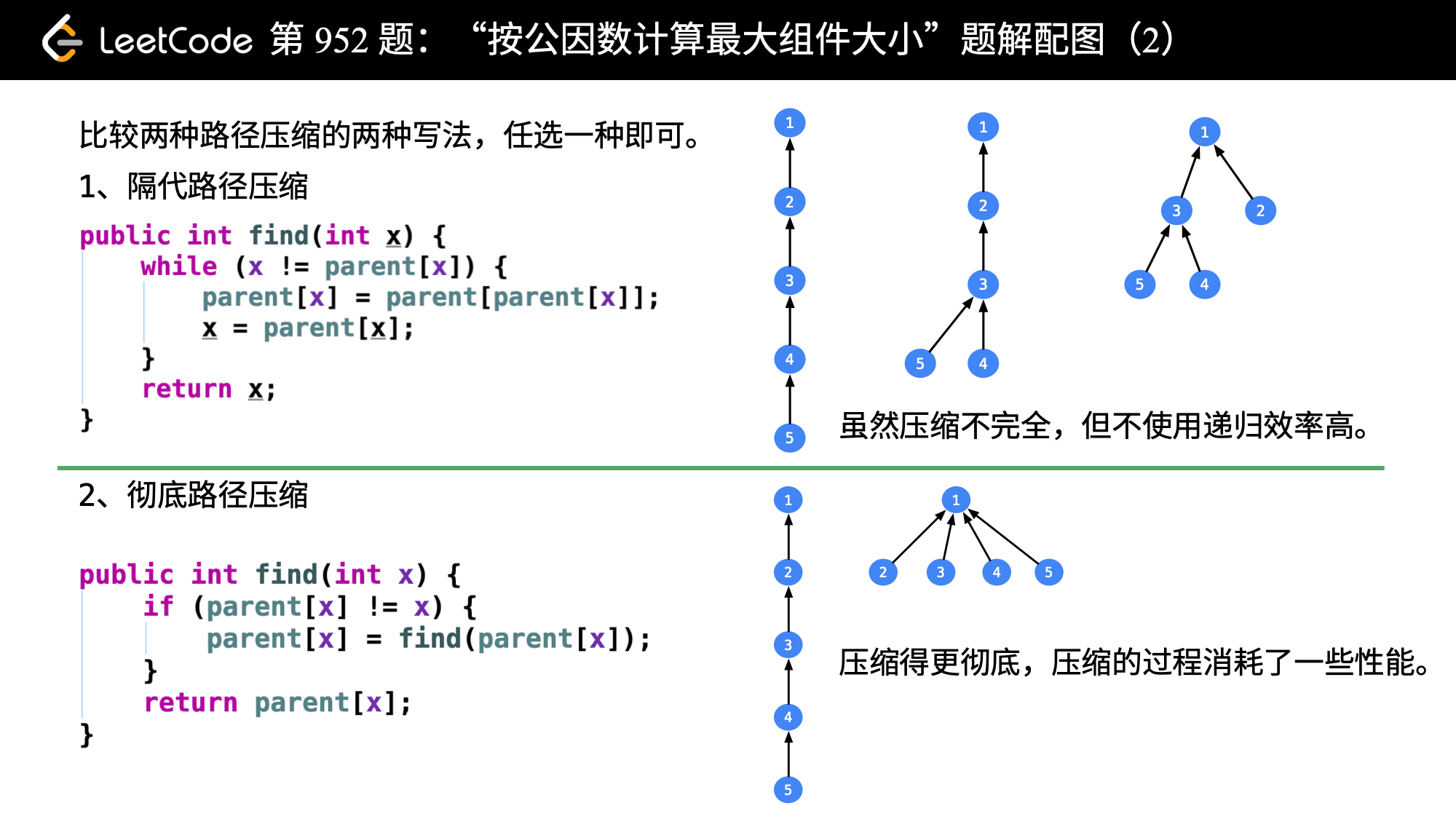
        // 使用了路径压缩
        public int find(int x) {
            if (parent[x] != x) {
                parent[x] = find(parent[x]);
            }
            return parent[x];
        }

        // 没有实现按秩合并
        public void union(int x, int y) {
            int rootX = find(x);
            int rootY = find(y);
            if (rootX != rootY) {
                parent[rootX] = rootY;
            }
        }
    }
}

Python 代码：

from math import sqrt
from typing import List


class Solution:

    def largestComponentSize(self, A: List[int]) -> int:

        class UnionFind:
            def __init__(self, n):
                self.parent = [i for i in range(n)]

            def union(self, x, y):
                root_x = self.find(x)
                root_y = self.find(y)
                if root_x != root_y:
                    self.parent[root_x] = root_y

            def find(self, x):
                while x != self.parent[x]:
                    self.parent[x] = self.parent[self.parent[x]]
                    x = self.parent[x]
                return x

        max_val = max(A)
        union_find = UnionFind(max_val + 1)

        for num in A:
            up_bound = int(sqrt(num))
            for i in range(2, up_bound + 1):
                if num % i == 0:
                    union_find.union(num, i)
                    union_find.union(num, num // i)

        cnt = [0 for _ in range(max_val + 1)]
        res = 0
        for num in A:
            root = union_find.find(num)
            cnt[root] += 1
            res = max(res, cnt[root])
        return res

C++ 代码：

#include <iostream>
#include <vector>
#include <math.h>
#include <unordered_map>

using namespace std;

class UnionFind {
private:
    vector<int> parent;
public:
    UnionFind(int n) : parent(n) {
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }

    void merge(int x, int y) {
        parent[find(x)] = parent[find(y)];
    }

    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }
};

class Solution {
public:
    int largestComponentSize(vector<int> &A) {
        int n = *max_element(begin(A), end(A));
        UnionFind unionFind(n + 1);

        for (int a: A) {
            for (int k = 2; k <= sqrt(a); k++) {
                if (a % k == 0) {
                    unionFind.merge(a, k);
                    unionFind.merge(a, a / k);
                }
            }
        }
        unordered_map<int, int> hashMap;
        int res = 1;
        for (int a:A) {
            res = max(res, ++hashMap[unionFind.find(a)]);
        }
        return res;
    }
};